The following article highlights the motivation and key findings our of Neurips 2020 paper titled “Efficient Exploration of Reward Functions in Inverse Reinforcement Learning via Bayesian Optimization”. You can find more details in our paper.
Ill-posed nature of IRL
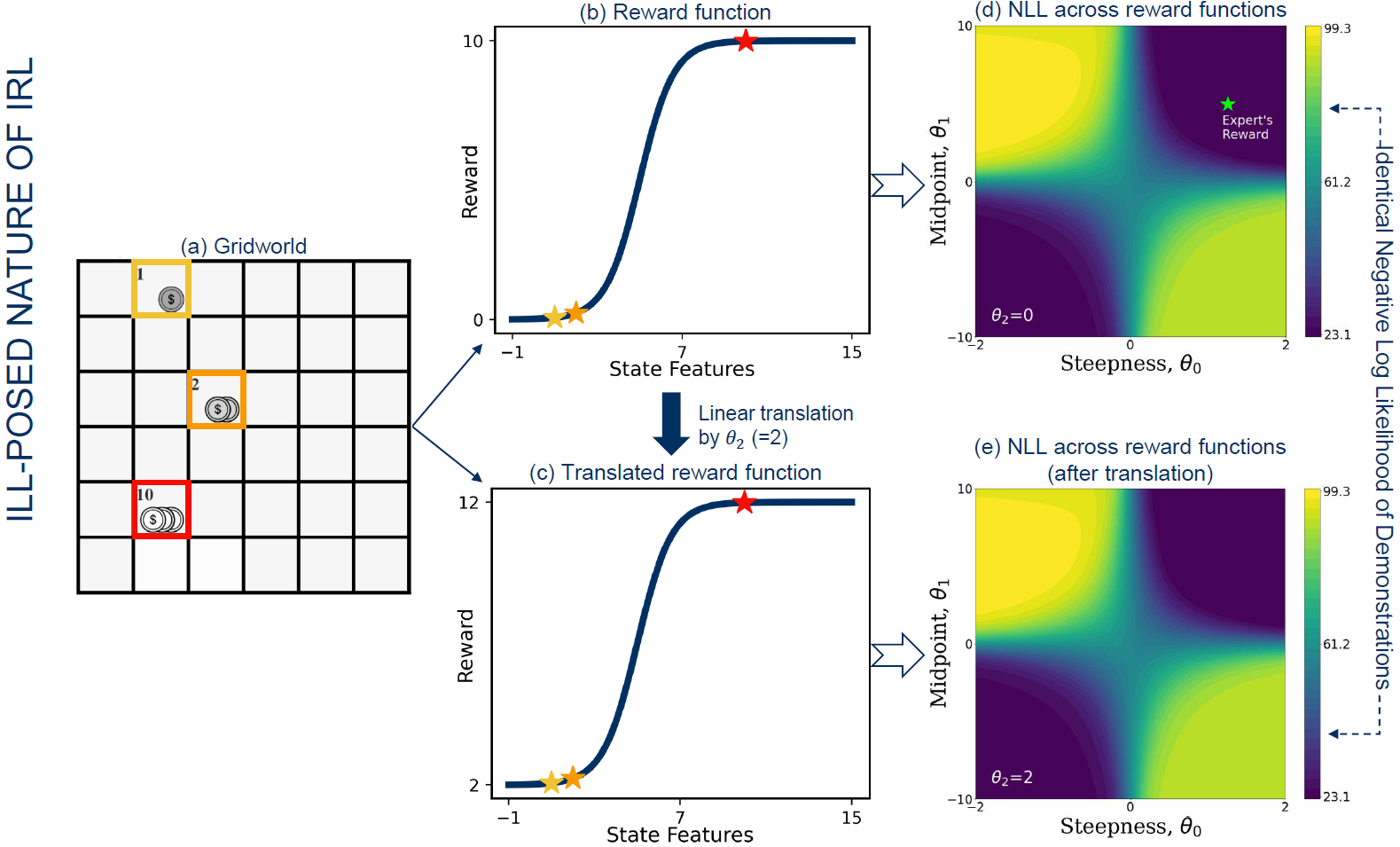
Inverse Reinforcement Learning (IRL) is an ill-posed problem as there typically exist many solutions(reward functions) for which a given behavior is optimal. This problem is made worse by policy-invariance where a reward function maintains its optimal policy under certain operations such as linear translation. Consider the example below. The reward function of the Gridworld (a) is a logistic function shown in (b). The steepness and midpoint of the curve as well as a linear translation value are the learnable reward function parameters. (d) shows the Negative Log Likelihood (NLL) of the expert demonstrations across various reward functions without any linear translation. Linearly translating (b) with a value of 2 gives rise to (c) which has identical NLL values (e) due to policy invariance.
Given the ill-posed nature of IRL, we adopt the perspective that an IRL algorithm should characterizethe space of solutions rather than output a single answer. However, blindly exploring the reward function space in search of optimal solutions is inefficient. For an efficient exploration, we turn to Bayesian Optimization (BO).
BO-IRL: Bayesian Optimization for IRL
We propose a novel approach to IRL, called BO-IRL, that utilizes Bayesian optimization (BO) to minimize the negative log-likelihood (NLL) of the expert demonstrations with respect to reward functions. BO is specifically designed for optimizing expensive functions by strategically picking inputs to evaluate and appears to be a natural fit for this task. Unfortunately, BO cannot be naively applied to IRL as the standard kernels available are unsuitable for representing the covariance structure in the space of reward functions. In particular they ignore policy invariance and therefore, require further exploration of the reward function space (example presented in the next section).
𝜌-RBF kernel
To tackle the above mentioned issue, we propose 𝜌-RBF kernel that handles policy invariance by using 𝜌-projection. 𝜌-projection maps reward functions to a 𝜌-space where (a) policy invariant reward functions are mapped to a single point and (b) reward functions with similar NLL are mapped to points close to each other. 𝜌-projection of reward is given by:
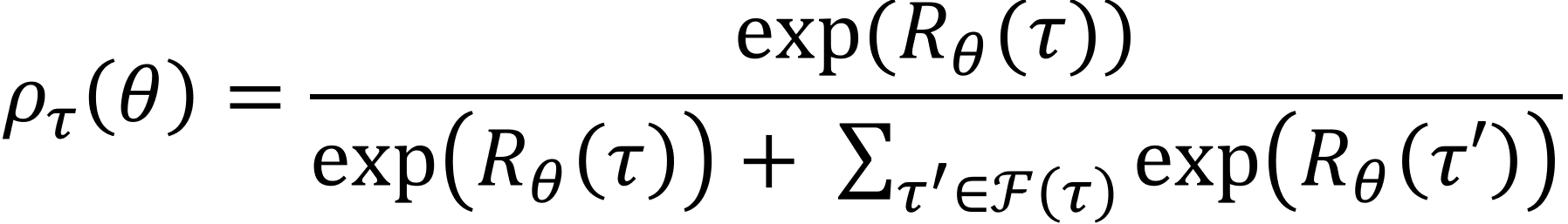
where: 𝜏 is an expert trajectory and is a set of trajectories from a uniform policy with the same starting state and length as 𝜏. RBF kernel is then applied to the 𝜌-space to capture the correlation between reward functions.
The following illustrates 𝜌-projection in action. Figures (a) and (b) represent NLL values of two sets of policy invariant reward functions that are linearly translated. (c) shows the corresponding 𝜌-space where the policy invariant reward functions (yellow stars) are mapped to the same point and points that are close in its range correspond to reward functions with similar NLL (red, yellow and blue stars).
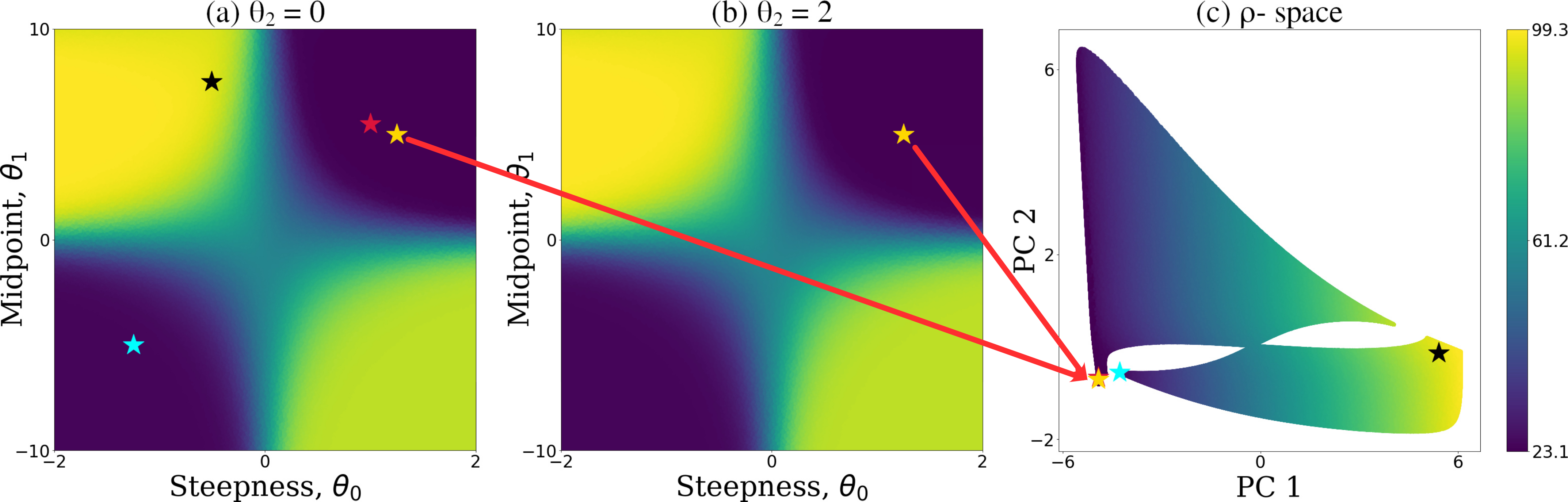
BO-IRL with 𝜌-RBF follows standard BO practices with Expected Improvement (EI) as the acquisition function.
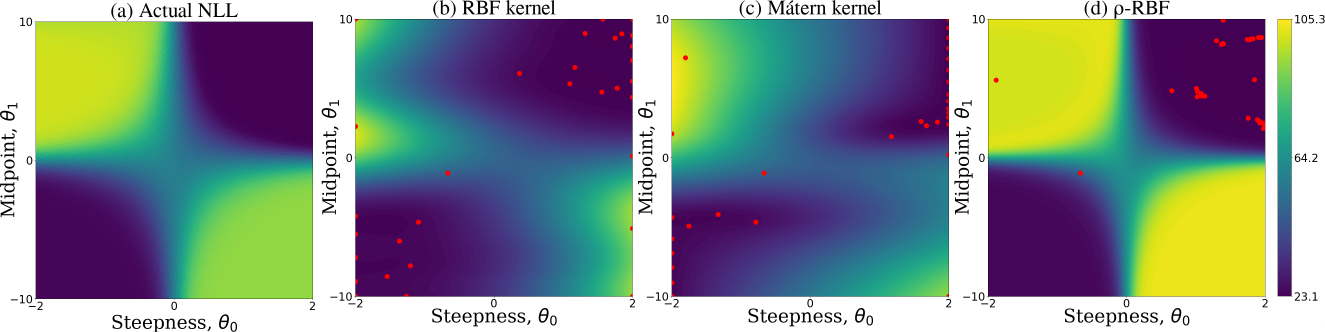
The following figure compares the learned posterior distribution over the NLL across reward functions for various kernels. As expected, 𝜌-RBF recovers the underlying structure of the reward function space without having to explore the entire space.
Evaluating BO-IRL
The following figure shows the environments used to evaluate BO-IRL. We applied BO-IRL to two discrete environments ((a) and (b)) and two continuous environments ((c) and (d)).
Uncovering multiple regions of high likelihood
We compared the posterior over the NLL obtained by BO-IRL to the posterior distribution over rewards obtained by Bayesian IRL to see whether these alrorithms have correctly identified regions of high likelihood. The following shows the results for the two discrete environment.
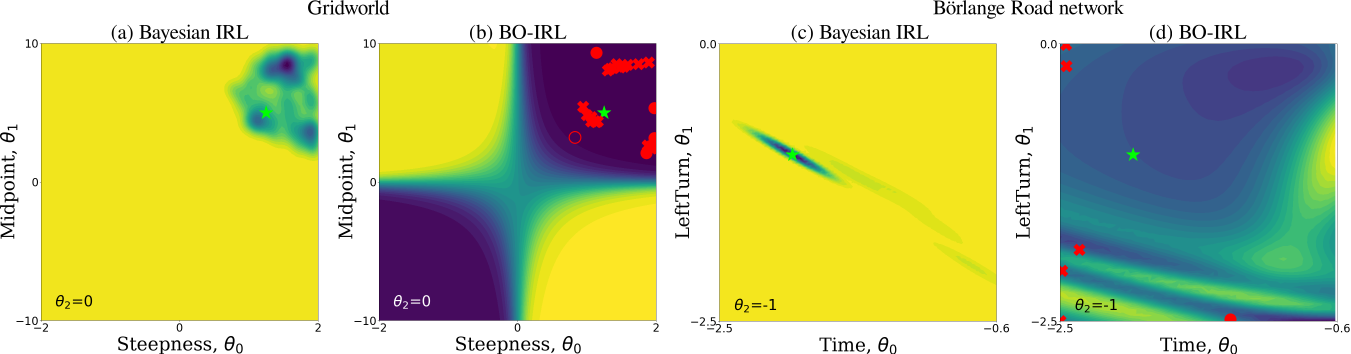BIRL assigns high probability to reward functions adjacent to the ground truth (green star) but ignores other equally probable regions. In contrast, BOIRL has identified multiple regions of high likelihood, as shown in (b) and (d). Interestingly, BO-IRL has managed to identify multiple reward functions with lower NLL than the expert’s true reward (as shown by red crosses) in both environments.
Number of evaluations
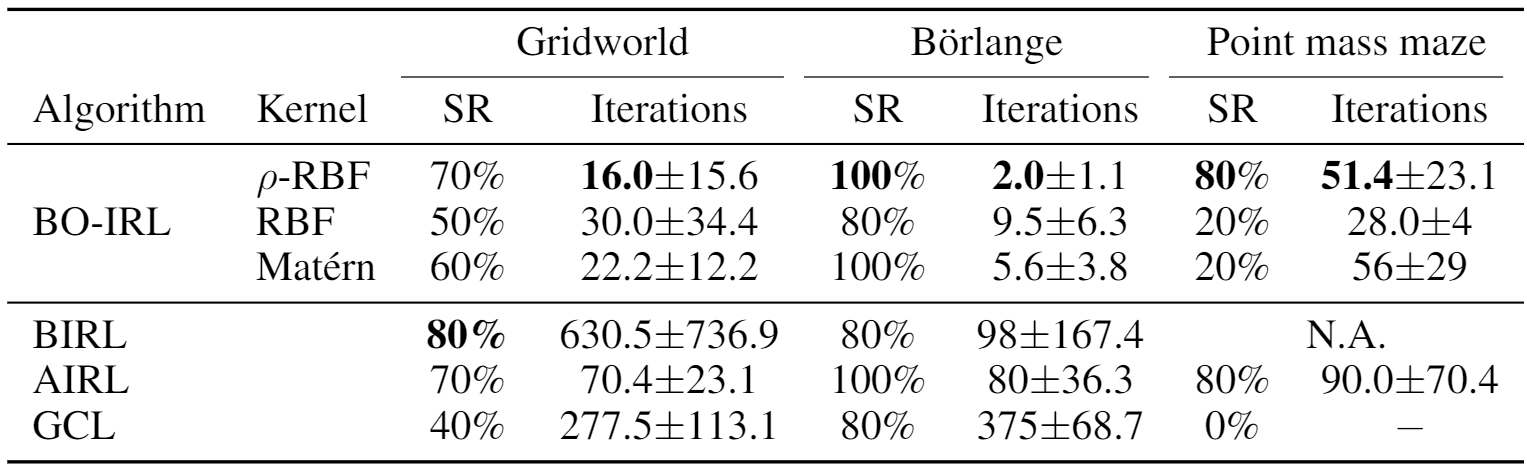
We evaluated the success rate (SR) and iterations required for various IRL algorithms to achieve the expert’s expected sum of rewards (ESOR) in three of the environments. The following table shows that BO-IRL with 𝜌-RBF kernel reached expert’s ESOR with fewer iterations than the other tested algorithms across all the settings. Further details can be found in the paper.
The following video shows BO-IRL being applied to the Fetch-Reach environment. The learned parameters are the distance threshold around the goal (indicated in blue circle) and a penalty imposed when outside the threshold. Within 11 iterations, the robot learns the expert’s reward. Specifically, this reward imposes a small region of threshold around the goal. Interesting, as the training progresses, the robot identifies more rewards that have higher likelihood than the expert’s reward. For instance, by iteration 90, the robot has discovered that the expert’s behavior can be achieved by having a wide threshold region and adjusting the penalty accordingly.
Resources
- Please find the code associated with this paper at this link
- The NeurIPS 2020 poster can be found here
Consider citing our paper if you build upon our results and ideas.
Balakrishnan, Sreejith, et al. “Efficient Exploration of Reward Functions in Inverse Reinforcement Learning via Bayesian Optimization.” Advances in Neural Information Processing Systems, 2020.
@article{balakrishnan2020efficient,
title={Efficient Exploration of Reward Functions in Inverse Reinforcement Learning via Bayesian Optimization},
author={Balakrishnan, Sreejith and Nguyen, Quoc Phong and Low, Bryan Kian Hsiang and Soh, Harold},
journal={Advances in Neural Information Processing Systems},
volume={33},
year={2020}
}
Contact
If you have questions or comments, please contact Sreejith Balakrishnan.
Acknowledgements
This research/project is supported by the National Research Foundation, Prime Minister’s Office, Singapore under its Campus for Research Excellence and Technological Enterprise (CREATE) program, Singapore-MIT Alliance for Research and Technology (SMART) Future Urban Mobility (FM) IRG and the National Research Foundation, Singapore under its AI Singapore Programme (AISG Award No: AISG-RP-2019-011).
