Know When to Abstain: Optimal Selective Classification with Likelihood Ratios, Alvin Heng★, Harold Soh★, arXiv preprint
Links:
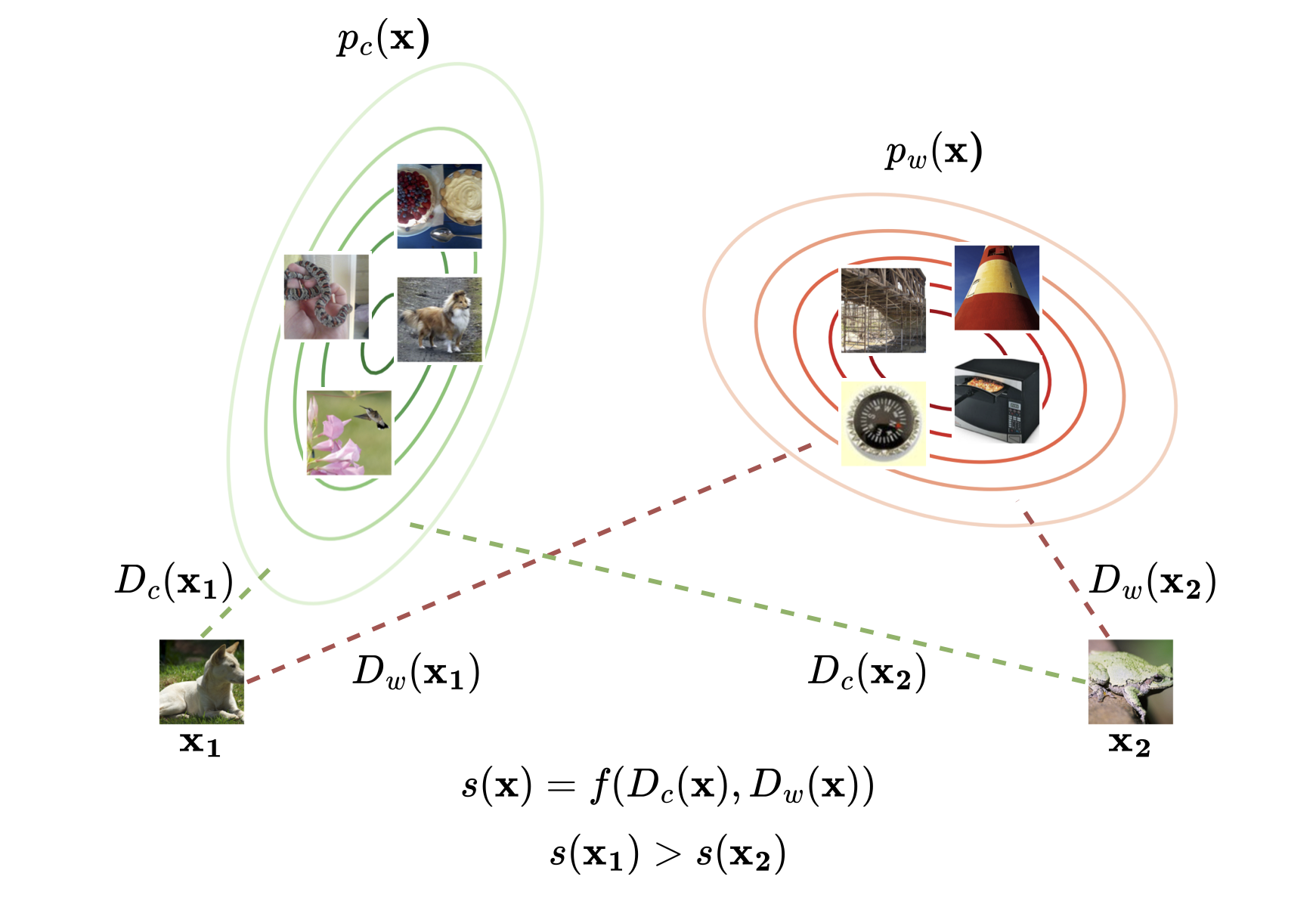
Selective classification enhances the reliability of predictive models by allowing them to abstain from making uncertain predictions. In this work, we revisit the design of optimal selection functions through the lens of the Neyman–Pearson lemma, a classical result in statistics that characterizes the optimal rejection rule as a likelihood ratio test. We show that this perspective not only unifies the behavior of several post-hoc selection baselines, but also motivates new approaches to selective classification which we propose here. A central focus of our work is the setting of covariate shift, where the input distribution at test time differs from that at training. This realistic and challenging scenario remains relatively underexplored in the context of selective classification. We evaluate our proposed methods across a range of vision and language tasks, including both supervised learning and vision-language models. Our experiments demonstrate that our Neyman-Pearson-informed methods consistently outperform existing baselines, indicating that likelihood ratio-based selection offers a robust mechanism for improving selective classification under covariate shifts.
Resources
You can find our paper here. Check out our repository here on github
Citation
Please consider citing our paper if you build upon our results and ideas.
Alvin Heng★, Harold Soh★, “Know When to Abstain: Optimal Selective Classification with Likelihood Ratios”, arXiv preprint
@article{heng2025know,
title={Know When to Abstain: Optimal Selective Classification with Likelihood Ratios},
author={Heng, Alvin and Soh, Harold},
journal={arXiv preprint arXiv:2505.15008},
year={2025} }
Contact
If you have questions or comments, please contact Alvin or Harold.
Acknowledgements
This research is supported by A*STAR under its National Robotics Programme (NRP) (Award M23NBK0053).