In this work, we contribute a new technique for improving the quality of samples from deep generative models. Even state-of-the-art generative models can produce samples of inconsistent quality. For example, the following images were generated from a SN-ResNet-GAN trained on the CIFAR10 dataset.
Some of the images are clearly discernible: we see a ship (4th), truck (5th), and horse (right-most). But the rest of the images do not appear realistic.
Our technique, Discriminator Gradient $f$low (DG$f$low), refines samples from GANs (and other deep generative models such as VAEs and normalizing flows!). Applying DG$f$low improves the samples above:
DG$f$low works by leveraging upon the discriminator. Our key insight is that sample refinement can be reformulated using the gradient flow of entropy-regularized $f$-divergences between the generated and real data distributions. The gradient flow has a Stochastic Differential Equation (SDE) counterpart which can be simulated using the density-ratio estimate provided by a discriminator. As the SDE is simulated, sample quality improves.
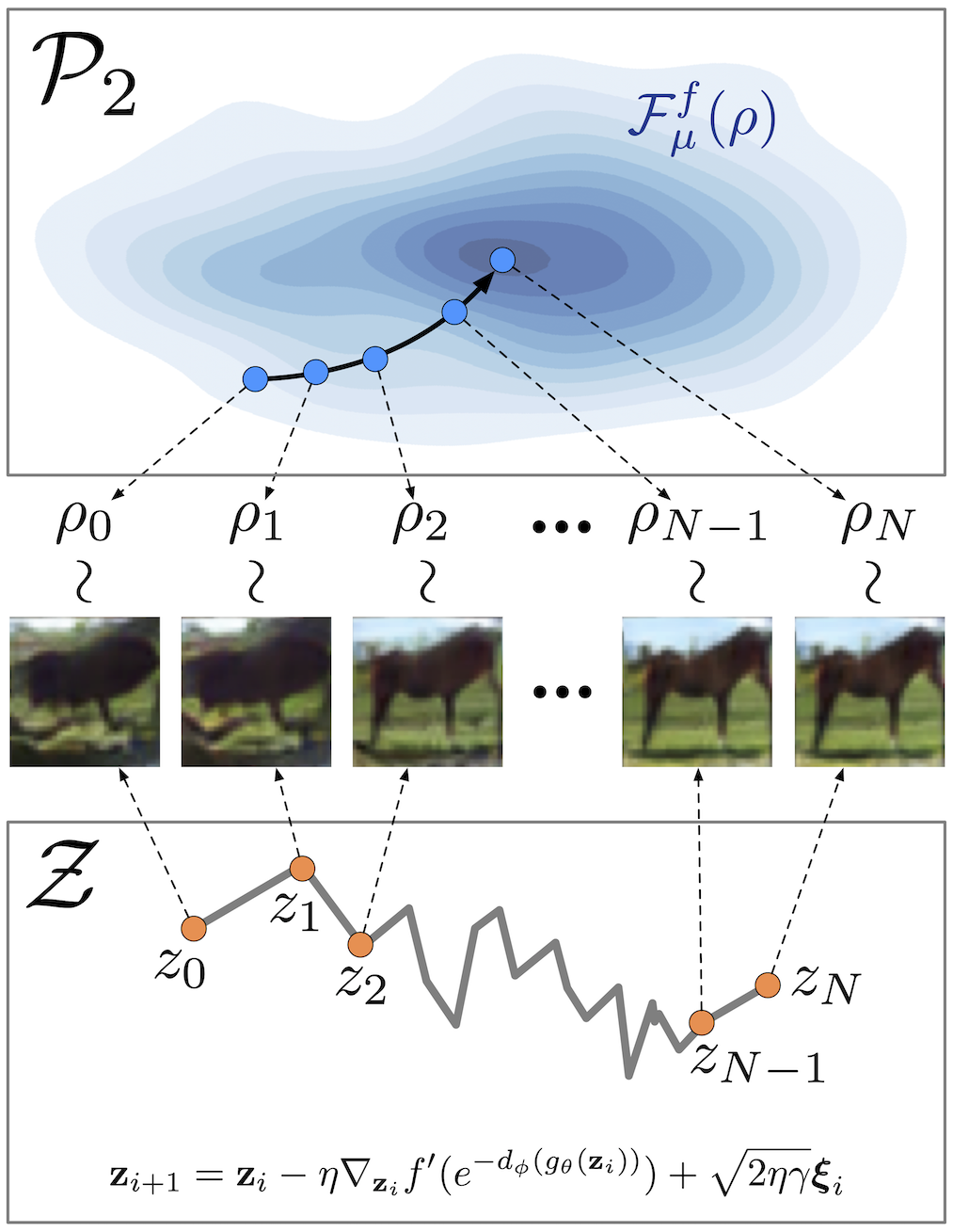Fig 4. An illustration of refinement using DGflow, with the gradient flow in the 2-Wasserstein space (top) and the corresponding discretized SDE in the latent space (bottom).
This formulation results in a surprisingly simple algorithm:
Algorithm 1. Sample refinement in the latent space using DG$f$low.
Algorithm 1 above is simple to implement and, with a few tricks, can be applied to different types of generators (e.g., VAEs and Normalizing Flows). The animation below shows how the images improve over the iterations in Algorithm 1:
DG$f$low theoretically generalizes and empirically outperforms Discriminator Optimal Transport [2] and Discriminator Driven Latent Sampling [4]. Read on below for more details about the key ideas and our experimental findings. Or have a look at our paper which has more complete information.
Preliminaries: Gradient Flow of Entropy-Regularized f-divergences
The gradient flow of a smooth energy function \(F: \mathcal{X} \to \mathbb{R}\) on the Euclidean space \((\mathcal{X}, \|\cdot\|_2)\) is the smooth curve \(\{\mathbf{x}_t\}_{t \in \mathbb{R}_{+}}\) the follows the direction of steepest descent of $F$, i.e.,
\begin{equation} \mathbf{x}’(t) = -\nabla F(\mathbf{x}(t)). \end{equation}
The idea of steepest descent curves can be extended to the 2-Wasserstein space — the space of probability measures with finite second moments — using the minimizing movement scheme. The gradient flow of a functional \(\mathcal{F}\) defined on the 2-Wasserstein space satisfies the continuity equation,
\begin{equation} \partial_t \rho_t + \nabla\cdot(\rho_t\mathbf{v}_t) = 0, \label{eq:cont-eq} \end{equation}
with the velocity field \(\mathbf{v}_t\) given by,
\begin{equation} \mathbf{v}_t = \nabla_{\mathbf{x}}\frac{\delta\mathcal{F}}{\delta\rho}(\rho), \label{eq:velocity} \end{equation}
where \(\frac{\delta\mathcal{F}}{\delta\rho}\) denotes the first variation of the functional \(\mathcal{F}\). We refer the reader to this blog post for an introduction to gradient flows in the 2-Wasserstein space.
We will now construct the gradient flow of the entropy-regularized $f$-divergence functional,
\begin{equation} \mathcal{F}_\mu^f \triangleq \mathcal{D}_f(\mu|\rho) - \gamma\mathcal{H}(\rho), \end{equation}
where \(\mu\) is the density of the real data distribution, \(\mathcal{D}_f(\mu\|\rho)\) is the \(f\)-divergence between \(\mu\) and \(\rho\), \(\mathcal{H}(\rho)\) denotes the entropy of \(\rho\). As the gradient flow is a steepest descent curve, the \(f\)-divergence term ensures that the “distance” between \(\mu\) and \(\rho\) decreases along the gradient flow and the entropy term results in improved diversity.
Using Eqs. ($\ref{eq:cont-eq}$) and ($\ref{eq:velocity}$), the gradient flow of \(\mathcal{F}_\mu^f\) can be derived to be the following PDE,
\begin{equation} \partial_t\rho_t(\mathbf{x}) - \nabla_\mathbf{x}\cdot\left(\rho_t(\mathbf{x})\nabla_\mathbf{x} f’\left(\rho_t(\mathbf{x})/\mu(\mathbf{x})\right)\right) - \gamma\Delta\rho_t(\mathbf{x}) = 0, \label{eq:f-div-grad-flow} \end{equation}
where \(\Delta\) denotes the Laplace operator.
Discriminator Gradient flow
Eq. (\(\ref{eq:f-div-grad-flow}\)) is a type of Fokker-Plank equation (FPE) which has an SDE counterpart given by,
\begin{equation} d\mathbf{x}_t = \underset{\textit{drift}}{\underbrace{-\nabla_\mathbf{x} f’\left(\rho_t/\mu\right)(\mathbf{x}_t)dt}}+\underset{\textit{diffusion}}{\underbrace{\sqrt{2\gamma}d\mathbf{w}_t}}, \label{eq:f-div-sde} \end{equation}
which defines the evolution of a particle $\mathbf{x}_t$ under the influence of drift and diffusion. Consequently, samples from the density $\rho_t$ along the gradient flow can be obtained by first drawing samples $\mathbf{x}_0 \sim \rho_0$ and then simulating the SDE in Eq. (\ref{eq:f-div-sde}) using a numerical method such as the Euler-Maruyama method.
If we let $\rho_0$ be the density of samples generated from a generative model, the samples can be pushed closer to the target density \(\mu\) by simulating Eq. (\ref{eq:f-div-sde}). This requires an estimate of the density-ratio \(\rho_t(\mathbf{x}_t)/\mu(\mathbf{x}_t)\) which can be approximated by \(\rho_0(\mathbf{x}_t)/\mu(\mathbf{x}_t)\) using a discriminator (binary classifier) trained on samples from \(\rho_0\) and \(\mu\) as follows,
\begin{equation} \rho_{\tau_0}(\mathbf{x})/\mu(\mathbf{x}) = \frac{1-D(y=1|\mathbf{x})}{D(y=1|\mathbf{x})} = \exp(-d(\mathbf{x})), \label{eq:density-ratio-trick} \end{equation}
where $d(\mathbf{x})$ denotes the logit output from the discriminator. Such a discriminator is readily available for GANs with scalar-valued critics such as SNGAN and WGAN variants. We term this procedure where samples are refined via gradient flow of $f$-divergences as Discriminator Gradient $f$low (DG$f$low).
Simulating DGflow in the Latent Space
During our preliminary experiments we observed that simulating the SDE in the high-dimensional data space using the stale estimate of the density-ratio \(\rho_t(\mathbf{x}_t)/\mu(\mathbf{x}_t) \approx\) \(\rho_0(\mathbf{x}_t)/\mu(\mathbf{x}_t)\) led to a degradation in the quality of samples for real-world image datasets (e.g., appearance of pixel artifacts). To tackle this problem, we propose refining the latent vectors before mapping them to samples in data-space using the generative model \(g_\theta\). The latent vectors are refined by simulating the following SDE,
\begin{equation} d\mathbf{z}_t = -\nabla_\mathbf{z} f’(p_Z/p_{\hat{Z}})(\mathbf{z}_t)dt + \sqrt{2\gamma}d\mathbf{w}_t, \end{equation}
where \(p_Z(\mathbf{z})\) is the density of the prior distribution and \(p_{\hat{Z}}(\mathbf{z})\) is the density of the target distribution in the latent space, i.e., it is the density of a probability measure whose pushforward under \(g_\theta\) approximately equals the target data density $\mu$. We show in our paper that the density-ratio \(p_Z(\mathbf{z})/p_{\hat{Z}}(\mathbf{z})\) can be approximated as
\begin{equation} \frac{p_{Z}(\mathbf{z})}{p_{\hat{Z}}(\mathbf{z})} = \frac{\rho_{0}(g_\theta(\mathbf{z}))}{\mu(g_\theta(\mathbf{z}))} = \exp(-d(g_\theta(\mathbf{z}))). \end{equation}
Refinement for all! Extending DGflow to Other Deep Generative Models
Now that we can improve sample quality of GANs, what about other deep generative models? Let $p_\theta$ be the density of the samples generated by a generator $g_\theta$ and $\mu$ be the density of the real data distribution. We are interested in refining samples from $g_\theta$; however, a corresponding density-ratio estimator for $p_\theta/\mu$ is unavailable for generative models such as GANs with vector-valued critics, VAEs, and Normalizing Flows. We employ a pretrained generator-discriminator pair to approximate the density-ratio $p_\theta/\mu$ as follows. Let ($g_\phi$, $D_\phi$) be a generator-discriminator pair that has been trained on the same dataset as $g_\theta$ (e.g., let $g_\phi$ and $D_\phi$ be the generator and discriminator of SNGAN respectively). We initialize another discriminator $D_\lambda$ with the weights from $D_\phi$ and fine-tune it on samples from $g_\phi$ and $g_\theta$. The density-ratio $p_\theta/\mu$ can now be approximated using a telescoping product,
\begin{equation} \frac{p_\theta(\mathbf{x})}{\mu(\mathbf{x})} = \frac{p_\phi(\mathbf{x})}{\mu(\mathbf{x})}\frac{p_\theta(\mathbf{x})}{p_\phi(\mathbf{x})} = \exp(-d_\phi(\mathbf{x}))\cdot\exp(-d_\lambda(\mathbf{x})), \end{equation}
where $d_\phi$ and $d_\lambda$ are logits output from $D_\phi$ and $D_\lambda$ respectively.
Qualitative Results
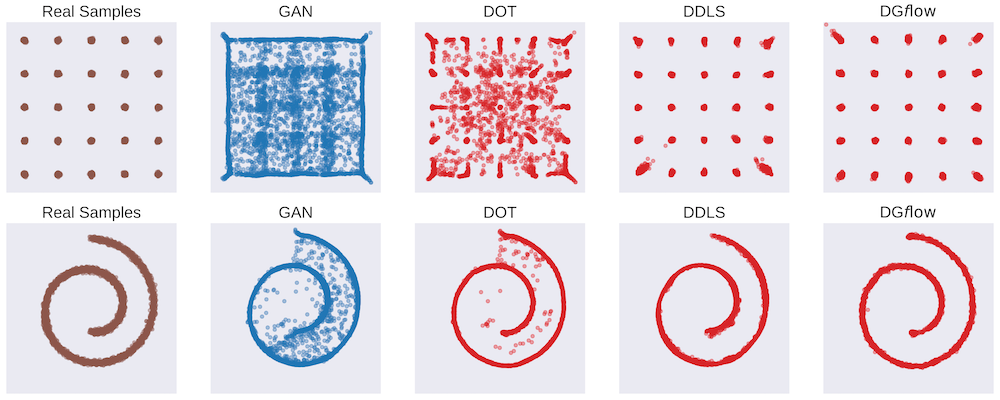
DG$f$low outperforms baseline methods of sample improvement on multiple generative models for the CIFAR10 and STL10 image datasets. DG$f$low also leads to significant improvement in the quality of samples for models without corresponding discriminators, namely MMDGAN, OCFGAN, VAE, and Glow. We refer the reader to the paper for quantitative results and present qualitative results in this article. Figure 2 shows that DG$f$low is able to correct almost all spurious samples generated by the base GAN generator and is able to recover the correct structure of the data. On generative models for images, DG$f$low improves the vibrance of the samples and corrects deformations in the foreground object as shown in Figure 3.
over the steps of DGflow for the CIFAR10 (left) and STL10 (right) datasets.
Code
Code for reproducing experiments presented in this paper can be found at this Github repo.
Citation
If you find our code or the ideas presented in our paper useful for your research, consider citing our paper.
Ansari, Abdul Fatir, Ming Liang Ang, and Harold Soh. “Refining Deep Generative Models via Discriminator Gradient Flow.” International Conference on Learning Representations, 2021.
@inproceedings{fatir2021refining,
title={Refining Deep Generative Models via Discriminator Gradient Flow},
author={Ansari, Abdul Fatir and Ang, Ming Liang and Soh, Harold},
booktitle={International Conference on Learning Representations (ICLR)},
year={2021}}
Contact
If you have questions or comments, please contact Abdul Fatir.
Acknowledgements
This research is supported by the National Research Foundation Singapore under its AI Singapore Programme (Award Number: AISG-RP-2019-011).
References
- Ryan Turner, Jane Hung, Eric Frank, Yunus Saatchi, and Jason Yosinski. Metropolis-Hastings generative adversarial networks. In ICML, 2019.
- Akinori Tanaka. Discriminator optimal transport. In NeurIPS, 2019.
- Samaneh Azadi, Catherine Olsson, Trevor Darrell, Ian Goodfellow, and Augustus Odena. Discriminator rejection sampling. In ICLR, 2019.
- Tong Che, Ruixiang Zhang, Jascha Sohl-Dickstein, Hugo Larochelle, Liam Paull, Yuan Cao, and Yoshua Bengio. Your GAN is secretly an energy-based model and you should use discriminator driven latent sampling. In NeurIPS, 2020.
