Safety-Constrained Policy Transfer with Successor Features

Safety-Constrained Policy Transfer with Successor Features, Zeyu Feng★, Bowen Zhang★, Jianxin Bi★, Harold Soh★, IEEE International Conference on Robotics and Automation (ICRA), 2023
Links: Paper | Github

Reinforcement learning (RL) remains challenging to employ in environments where interactions are costly and safety is a principal concern. In this work, we contribute a new technique for transferring safety-constrained policies across tasks with different objectives. Our method, called Successor Feature Transfer for Constrained Policies (SFT-CoP), utilizes constrained optimization and transfer learning to promote safe behavior through both sample reduction and constraint adherence during RL training.

Preliminaries: Constrained Markov Decision Processes (CMDPs) and Successor Features (SFs)

SFT-CoP considers policy transfer in CMDPs [1]. The main distinction between a CMDP \(M^c = (\mathcal{S}, \mathcal{A}, p, r, c, \gamma, \tau)\) and a conventional MDP is that CMDP includes an additional utility function \(c(s,a,s^{\prime})\) to account for safety considerations. This allows CMDPs to cleanly separate task goals from safety considerations. Unlike prior work on risk-aware policy transfer [2], it can encompass cases where risk cannot be captured by the variance of the return and enables the specification of a wide variety of safety considerations. The optimization goal in CMDP is to obtain an optimal policy that maximizes the expected reward return while ensuring the expected utility return is met,

\begin{equation} \max_{\pi\in\Pi} \quad V_r^{\pi}\left(s_0\right) \quad\quad\quad \text{s.t.} \quad V_c^{\pi}\left(s_0\right) \geq \tau, \end{equation}

where \(\tau\) is the threshold we seek to enforce for the constraint.

To transfer policies across tasks, we consider the task space spanned by reward and utility functions that are linear with respect to a shared feature function \(\phi\left(s,a,s^{\prime}\right)\in\mathbb{R}^d\)

\begin{equation} \mathcal{M}_{\phi}^c \left( \mathcal{S}, \mathcal{A}, p, \gamma\right) = \{ M^c\left(\mathcal{S}, \mathcal{A}, p, r_i, c_i, \gamma\right) \vert r_i\left(s,a,s^{\prime}\right) = \phi\left(s,a,s^{\prime}\right)^T w_{r,i}, c_i\left(s,a,s^{\prime}\right)=\phi\left(s,a,s^{\prime}\right)^T w_{c,i} \}. \end{equation}

The advantage of using this model is that the action-value function, e.g., for the reward function, is given by \(Q_{r,i}^{\pi_i}\left(s,a\right) = \psi^{\pi_i}\left(s,a\right)^{\top} w_{r,i}\), where \(\psi^{\pi_i}\) are the successor features [3]. In other words, we can quickly evaluate a policy \(\pi_i\) on a new task \(M_j^c\) by computing a dot-product. The SFs \(\psi^{\pi_i}\left(s,a\right)\) satisfy the Bellman equation and can be computed via dynamic programming, and \(w_{r,j}\) (\(w_{c,j}\) resp.) can be directly plugged-in (if known) or learned using standard learning algorithms.

Constrained Policy Transfer

With source policies learned on \(N\) source CMDP tasks using SFs, we can obtain policy evaluations on a target task \(M_j^c\), specifically approximated \(Q\)-functions \(\left\{ \tilde{Q}_{r,j}^{\pi_i} \right\}_{i=1}^N\) and \(\left\{ \tilde{Q}_{c,j}^{\pi_i} \right\}_{i=1}^N\). Inspired by the policy improvement in SFs, SFT-CoP proposes the following transfer policy for the target task

\begin{equation} \pi(s)\in\mathrm{argmin}_a\max_{i\in[N]} \left\{ \tilde{Q}_{r,j}^{\pi_i}(s,a) + \tilde{\lambda}_j \tilde{Q}_{c,j}^{\pi_i}(s,a) \right\}, \end{equation}

by specifying a \(\tilde{\lambda}_j\) for the new task. Denote by \(L\left(\pi, \lambda_j\right) = V_{r,j}^{\pi}\left(s\right) + \lambda_j\left( V_{c,j}^{\pi}\left(s\right) - \tau \right)\) and \(\lambda_j^* = \mathrm{argmin}_{\lambda_j\geq0} \max_{\pi\in\Pi}L\left(\pi, \lambda_j\right)\) the Lagrange and the optimal Lagrange multiplier (or dual variable) for the optimization problem in the target task, respectively. Under mild conditions, it can be shown that (Proposition 1 in paper) the difference between the Lagrange value of the transfer policy and that of optimal policy is upper bounded by several items. One major term \(\left\vert\lambda_j^*-\tilde{\lambda}_j\right\vert\) highlights the importance of obtaining a good estimate of the optimal dual variable for transfer in CMDPs. However, estimating it by training on the target task by primal dual optimization entails many interactions with the environment, defeating the purpose of transfer. Instead, we propose a practical optimization method to approximate \(\lambda_j^*\) without having to resort to RL on the target task.

Optimal Dual Estimation

Instead of optimizing over the entire policy space \(\Pi\), we can use the convex polygon \(\Pi_c := \texttt{Conv}\left(\{\tilde{\pi}_i\}_{i=1}^N\right)\) to approximate the optimal Lagrange multiplier by allowing stochastic combination of policies. Strong duality is also satisfied as a result of convexification. A policy \(\pi_{\alpha}(a\vert s) = \frac{\sum_{i=1}^n\alpha_i\rho^{\tilde{\pi}_i}(s,a)}{\int_{\mathcal{A}}\sum_{i=1}^n\alpha_i\rho^{\tilde{\pi}_i}(s,a)\text{d} a} \in \Pi_c\) has value function \(V_{r,j}^{\pi_{\alpha}}(s) = \sum_{i=1}^N\alpha_i V_{r,j}^{\tilde{\pi}_i}(s) = \sum_{i=1}^n\alpha_i\int_{\mathcal{S},\mathcal{A}}\rho^{\tilde{\pi}_i}(s,a)r_j(s,a)\text{d}s\text{d}a\), where \(\sum_{i=1}^N\alpha_i=1\), \(\alpha_i\geq0\) for any \(i\) and \(\rho^{\pi}(s,a)=\sum_{t=0}^{\infty}\gamma^t P(s_t=s,a_t=a\vert\pi)\) is occupation measure. The following algorithm shows the alternative updates used to compute \(\tilde{\lambda}_j^{\alpha} \in \mathrm{argmin}_{\lambda_j\geq0}\max_{\pi_{\alpha}\in\Pi_c} V_{r,j}^{\pi_{\alpha}}\left(s\right) + \lambda_j\left( V_{c,j}^{\pi_{\alpha}}\left(s\right) - \tau \right)\).

Algorithm 1. Estimation of the dual variable by alternative update for SFs transfer.

In a nutshell, SFT-CoP finds an approximation of the optimal dual variable by Algorithm 1 and uses the resulting \(\tilde{\lambda}_j^{\alpha}\) in the transfer policy, wherein the reward and utility weights can be learned with a few steps of finetuning if they are unknown.

One might wonders whether the above procedure can find a convergent solution for \(\tilde{\lambda}_j^{\alpha}\) due to sampling and gradient descent. Proposition 2 and 3 in our paper show that Algorithm 1 does converge asymptotically under proper conditions [4] of the learning rate \(\eta^{(t)}\).

Simulation Results

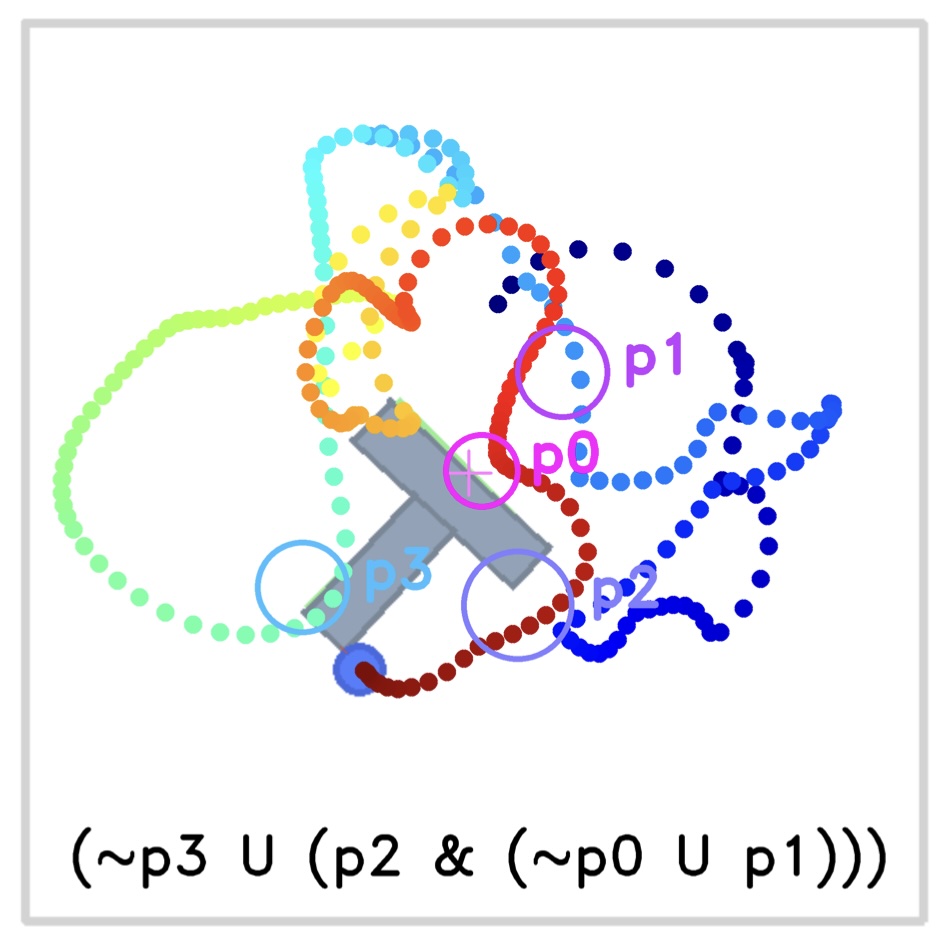
Using three simulated environments (Fig. 1), we compared SFT-CoP against state-of-the-art transfer learning baselines including SF Q-Learning (SFQL) and Risk-Aware SF Q-Learning (RASFQL) [4], and against safe RL methods including CPO and Primal-Dual Q-Learning (PDQL) which can be used to solve CMDPs with safety constraints.

Fig. 1: Benchmark domains used in our experiments.

Fig. 2 shows the trajectories of RASFQL and SFT-CoP in the four-room domain. As can be seen from the figures, the baseline risk-aware method was unable to avoid general cost constraints. Fig. 3 shows the performance when compared with other methods. In summary, SFT-CoP achieves positive transfer in terms of task objectives and constraints in safety-constrained settings.

Fig. 2: Trajectories of RASFQL (left) and SFT-CoP (right) on a same task (only blue circles and red triangles have positive rewards) from the Four-Room domain.

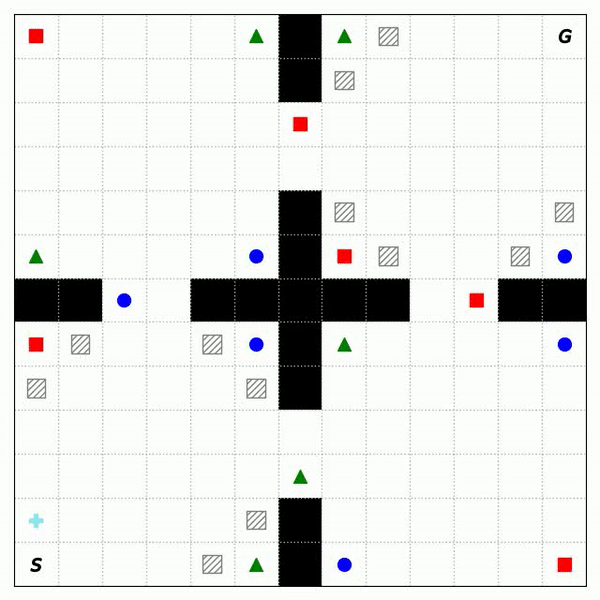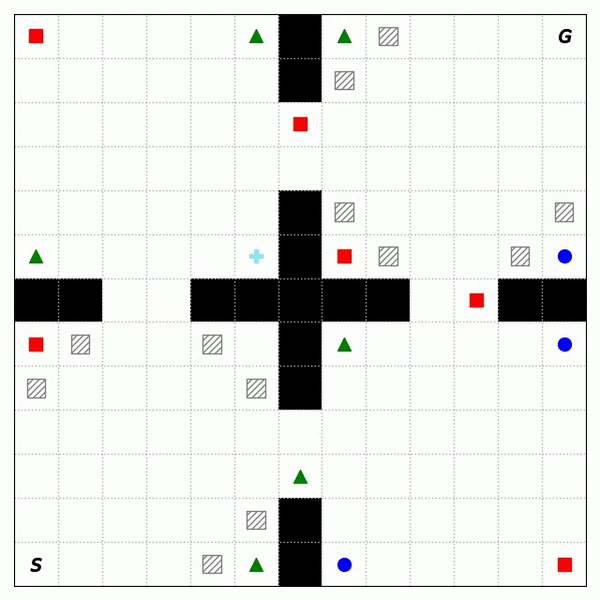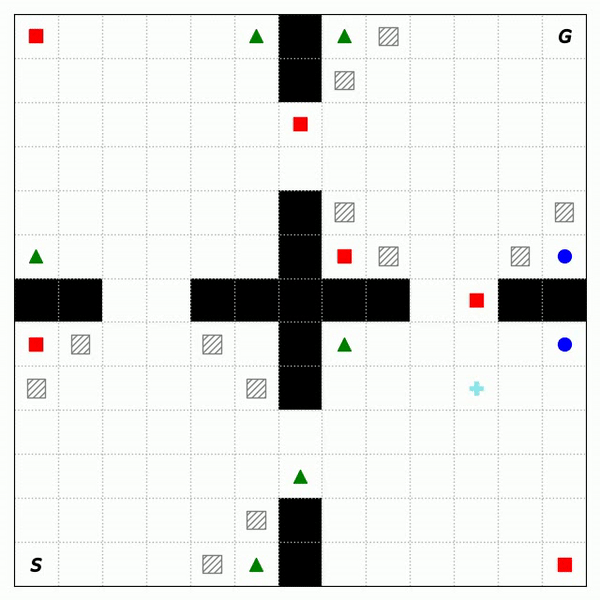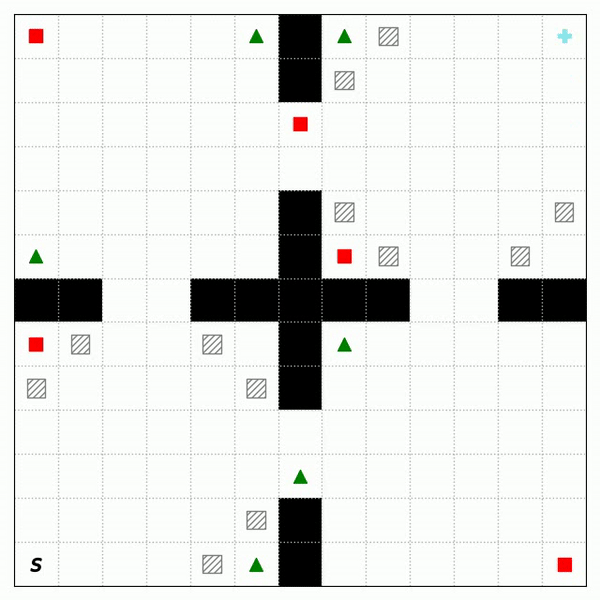
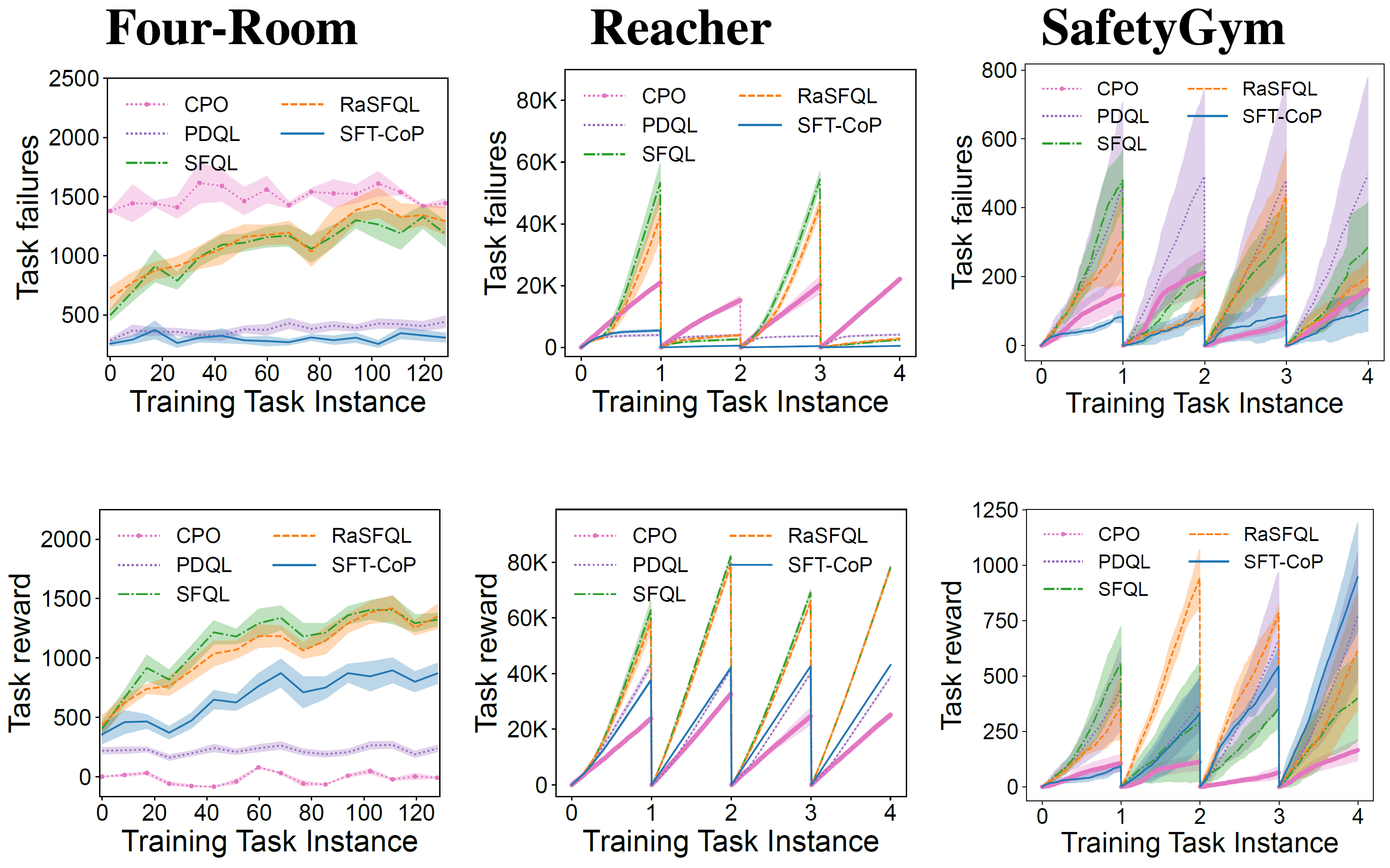Fig. 3: Performance of CPO, PDQL, SFQL, RASFQL and SFT-CoP on the Four-Room, Reacher and SafetyGym domains. We compare task failures (top row) and rewards (bottom row) between the different transfer methods over the training task instances.

Resources

You can find our paper here. Check out our repository here on github.

Citation

Please consider citing our paper if you build upon our results and ideas.

Zeyu Feng★, Bowen Zhang★, Jianxin Bi★, Harold Soh★, “Safety-Constrained Policy Transfer with Successor Features”, IEEE International Conference on Robotics and Automation (ICRA), 2023

@INPROCEEDINGS{fzbs2023,
author={Feng, Zeyu and Zhang, Bowen and Bi, Jianxin and Soh, Harold},
booktitle={2023 International Conference on Robotics and Automation (ICRA)},
title={Safety-Constrained Policy Transfer with Successor Features},
year={2023}}

Contact

If you have questions or comments, please contact zeyu.

Acknowledgements

This research is supported in part by the National Research Foundation (NRF), Singapore and DSO National Laboratories under the AI Singapore Program (Award Number: AISG2-RP-2020-017).

References

1. E. Altman, Constrained Markov Decision Processes. CRC Press, 1999, vol. 7.
2. M. Gimelfarb, A. Barreto, S. Sanner, and C.-G. Lee, “Risk-aware transfer in reinforcement learning using successor features,” in Advances in Neural Information Processing Systems, 2021.
3. A. Barreto, W. Dabney, R. Munos, J. J. Hunt, T. Schaul, H. P. van Hasselt, and D. Silver, “Successor features for transfer in reinforcement learning,” in Advances in Neural Information Processing Systems, vol. 30. Curran Associates, Inc., 2017.
4. K. M. Anstreicher and L. A. Wolsey, “Two “well-known” properties of subgradient optimization,” Mathematical Programming, vol. 120, no. 1, pp. 213–220, 2009.